A análise de Weibull é um método estatístico utilizado na engenharia de confiabilidade e manutenção para analisar dados de vida útil, taxas de falhas e confiabilidade de equipamentos. Nomeada em homenagem a Wallodi Weibull, quem descreveu este modelo estatístico, a distribuição de Weibull é versátil e pode descrever vários comportamentos de falha.
Aplicação da análise de Weibull na manutenção
A seguir, vamos mostrar como a aplicação ocorre no contexto da manutenção.
Análise de falhas
Ao ajustar os dados a uma distribuição de Weibull, a análise pode descrever diferentes tipos de falha, como a mortalidade infantil, falhas na vida útil normal ou falhas por desgaste. Isso se alinha bem com as diferentes fases da curva da banheira na confiabilidade.
Previsão de confiabilidade
A análise de Weibull ajuda a prever o comportamento futuro de falha de um componente ou sistema. Essa capacidade preditiva auxilia no planejamento das atividades de manutenção, reduzindo os tempos de inatividade não planejados e aumentando a eficiência geral do sistema.
Design e análise de garantias
Neste caso, engenheiros e fabricantes podem usar a análise de Weibull para estimar a confiabilidade dos equipamentos ou componentes dentro de um período de garantia específico. Isso auxilia na fase de design para fazer os ajustes necessários e atender aos objetivos desejados de confiabilidade.
Comparação entre diferentes equipamentos ou ativos
Ao ajustar diferentes conjuntos de dados às distribuições de Weibull, os gerentes de manutenção podem comparar a confiabilidade de diferentes ativos ou estratégias de manutenção. Isso ajuda nos processos de tomada de decisões relacionados à seleção de materiais, componentes ou abordagens de manutenção.
Planejamento de manutenção
A análise de Weibull pode fornecer informações valiosas sobre as características de falha de máquinas ou equipamentos. Essas informações permitem a formulação de estratégias, programando atividades de manutenção preventiva em intervalos ótimos para minimizar custos e maximizar o desempenho.
Avaliação de riscos
Permite avaliar o risco associado a diferentes modos de falha e auxilia na priorização de atividades de manutenção. As áreas de alto risco podem ser abordadas primeiro, garantindo segurança e conformidade com as normas regulatórias.
Parâmetros da distribuição de Weibull
Antes de entender o gráfico da distribuição de Weibull, é importante compreender alguns de seus parâmetros:
Parâmetro de Forma (β, Beta)
Este parâmetro descreve a forma de distribuição e caracteriza o modo de falha.
Por exemplo: β < 1 indica uma taxa de falha decrescente, β = 1 indica uma taxa de falha constante, e β > 1 indica uma taxa de falha crescente.
Parâmetro de Escala (η, Eta)
É um fator de escala que estica ou comprime a distribuição. Fornece uma estimativa da "vida característica" do produto, que é o tempo em que 63,2% dos equipamentos terão falhado.
Passos para construir o gráfico de Weibull
A seguir, são apresentados 8 passos para construir o gráfico usando dados de falha dos ativos que você deseja analisar.
Coletar dados: Reúna dados de falha para o ativo que está analisando. Você precisará dos tempos exatos de falha para cada equipamento ou ativo.
Ordenar dados: Organize os tempos de falha de menor para maior e atribua uma classificação (de 1 a n) para cada tempo de falha.
Calcular probabilidades de falha: Utilize o método das Faixas Medianas ou outros métodos para calcular as probabilidades de falha. Uma fórmula comum para isso é:
Fi = i / (n + 1)
Onde Fi é a probabilidade de falha, i é a faixa, e n é o número total de falhas
Transformar os dados: Calcule o logaritmo natural dos tempos de falha e o logaritmo natural do logaritmo natural negativo das probabilidades de falha.
x = ln(tempos de falha)
y= ln(−ln(1 − Fi))
Plotar os dados: Plote os dados transformados (x, y) em um gráfico normal ou utilize um software estático.
Ajustar uma linha: Usando regressão linear, ajuste uma linha reta aos dados. A inclinação da linha será o parâmetro de forma (β), e a interseção com o eixo x ajudará a encontrar o parâmetro de escala (η).
Interpretar os parâmetros: Use os valores estimados de β e η para entender o comportamento de falha do seu sistema e planejar estratégias de manutenção conforme necessário.
Exemplo prático
Vamos ver um exemplo de como usar a análise de Weibull para a manutenção.
Imagine que você tenha dados de falhas de um conjunto de 10 bombas idênticas. Veja como você poderia aplicar a análise de Weibull.
Calcular as probabilidades de falha
Para as 10 bombas idênticas, aqui estão os tempos de falha em horas:
| Faixa (i) | Tempos de falha (Ti) |
|---|---|
| 1 | 50 |
| 2 | 100 |
| 3 | 150 |
| 4 | 200 |
| 5 | 250 |
| 6 | 300 |
| 7 | 350 |
| 8 | 400 |
| 9 | 450 |
| 10 | 500 |
Para o cálculo das probabilidades de falha use o método de Faixas Medianas e, em seguida, faça a tabulação:
| Faixa (i) | Tempo de falha (Ti) | Probabilidade estimada (Fi) |
|---|---|---|
| 1 | 20 | 0.067 |
| 2 | 50 | 0.133 |
| 3 | 80 | 0.200 |
| 4 | 100 | 0.267 |
| 5 | 150 | 0.333 |
| 6 | 200 | 0.400 |
| 7 | 250 | 0.467 |
| 8 | 350 | 0.533 |
| 9 | 500 | 0.600 |
| 10 | 750 | 0.667 |
Transformar os dados
Nesta etapa, calculamos as coordenadas (x, y) utilizando o logaritmo natural dos tempos de falha e as probabilidades de falha.
| Faixa (i) | Tempo de falha (Ti) | Probabilidade estimada (Fi) | x = ln(Failure Time) | y = ln(-ln(1 - Fi)) |
|---|---|---|---|---|
| 1 | 20 | 0.067 | 2.996 | -4.201 |
| 2 | 50 | 0.133 | 3.912 | -3.504 |
| 3 | 80 | 0.200 | 4.382 | -2.996 |
| 4 | 100 | 0.267 | 4.605 | -2.590 |
| 5 | 150 | 0.333 | 5.010 | -2.251 |
| 6 | 200 | 0.400 | 5.298 | -1.961 |
| 7 | 250 | 0.467 | 5.521 | -1.704 |
| 8 | 350 | 0.533 | 5.857 | -1.473 |
| 9 | 500 | 0.600 | 6.214 | -1.255 |
| 10 | 750 | 0.667 | 6.620 | -1.048 |
Plotar os dados
Nesta etapa, os dados (x, y) são plotados e uma linha reta é ajustada usando regressão linear, conforme mostrado abaixo: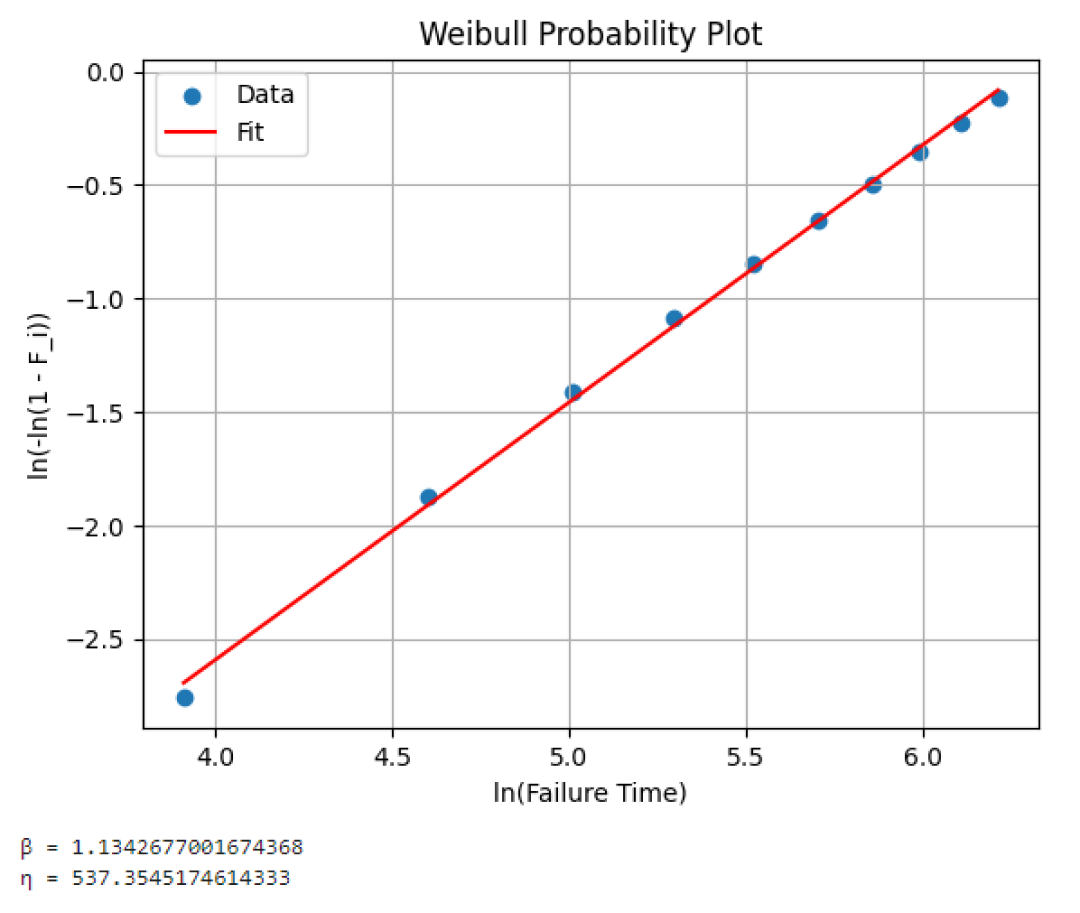
Interpretação dos parâmetros
Os parâmetros da análise de Weibull, β (parâmetro de forma) e η (parâmetro de escala), oferecem insights sobre a confiabilidade e as características de falha dos equipamentos ou sistemas em estudo.
Neste caso específico:
Parâmetro de Forma β=1.134
Um valor de β maior que 1 sugere que a taxa de falha aumenta com o tempo. Isso pode indicar que as falhas são principalmente devido ao envelhecimento. Dado que β está bastante próximo de 1, a taxa de falha pode estar aumentando relativamente lentamente com o tempo.
Parâmetro de Escala η=537.35
Este valor pode ser interpretado como o tempo em horas em que cerca de 63,2% das bombas terão falhado.
Concluindo, a análise de Weibull sugere que a taxa de falha está aumentando com o tempo, mas talvez a um ritmo mais lento. A vida característica do produto ou sistema indica o momento em que se espera que uma parte significativa da população falhe.
Essas informações podem ser vitais no planejamento de estratégias de manutenção, na definição de períodos de garantia e na compreensão da confiabilidade geral dos produtos ou componentes.

